一项关于电阻的最新发现
2020年7月31日,《自然通讯》(Nature Communications)发表了题为T-square resistivity without Umklapp scattering in dilute metallic Bi2O2Se的研究论文。西湖大学理学院特聘研究员林效为通讯作者,其课题组2018级博士生王嘉璐为第一作者,合作者有西湖大学理学院刘仕特聘研究员和任之特聘研究员,以及ESPCI Kamran Behnia教授。

日常生活中随处可见的材料具有不同大小的电阻,根据电阻率从低到高分为金属、半导体和绝缘体。对于导电性很好的金属,电阻是由电子散射导致的。一般来说,不同的温度区间内,电子散射机理不尽相同,因此电阻和温度的关系也不同(见图1)。在较高温度时(T>ΘD,声子德拜温度),电阻率随温度线性变化(ρ∝T);在中间温度区间内,电阻率呈现温度的五次方关系(ρ∝T5),这是电子受到声子(晶格振动)的散射产生的结果。随着温度进一步降低到液氦区间,电子不再受到声子散射影响,电子-电子散射行为占据主导,电阻率表现为温度的平方关系(ρ∝T2),电子间的相互作用可以用费米液体理论来描述。具体来说,低温下金属的电阻率可表示 为公式:ρ = ρ0+ AT2;其中,ρ0是剩余电阻率,由材料晶格缺陷导致,第二项是来自电子-电子散射。
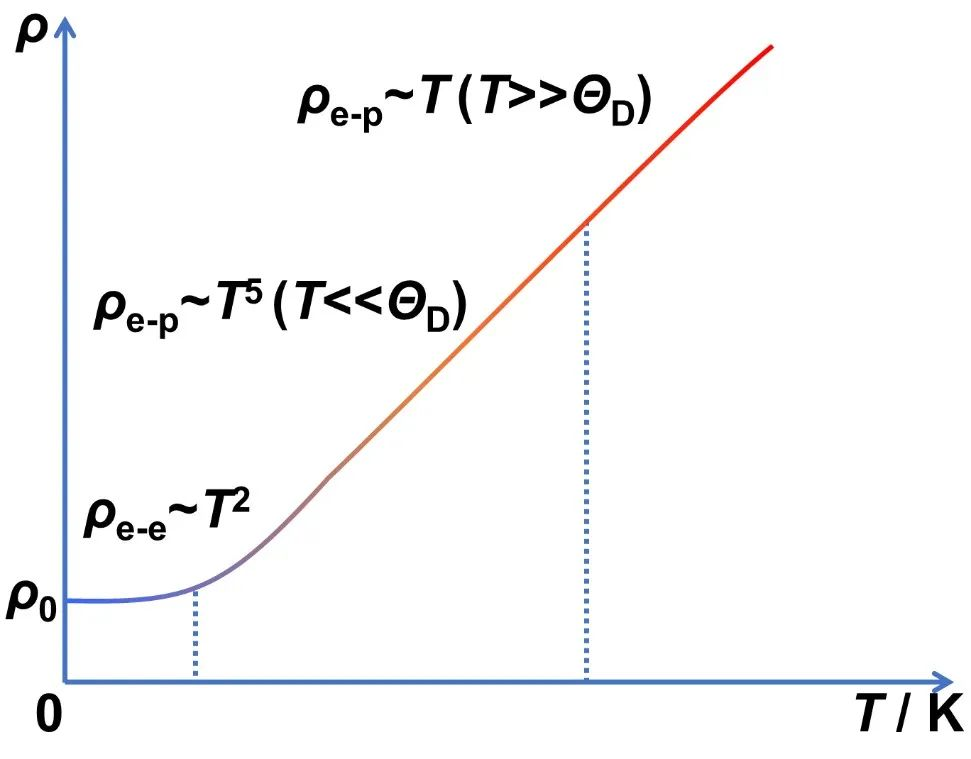
图1 电阻的产生是由于电子被散射。不同温度下,电子散射机制并不相同,因此电阻率和温度的关系也不同。
低温电阻率的温度平方关系是费米液体体系的普遍行为,几乎所有材料都可用费米液体电子散射机制完美解释。然而,近日西湖大学林效研究员和其合作者的研究结果表明,费米液体电子散射理论无法解释Bi2O2Se的电阻行为。
图2 Bi2O2Se的晶格结构
费米液体电子散射行为逃不出两种机制[1-4]:带间散射(inter-band散射)和Umklapp过程,见图3。
带间散射表述为隶属于不同能带的电子相互碰撞,由于质量不同,部分动量会被转移到晶格,最终导致电流衰减,产生电阻。
Umklapp过程要求体系具有较大的费米面及费米波矢,电子-电子碰撞之后,其中某一电子存在一定几率被散射到第二布里渊区,为回到第一布里渊区,体系会转移一定动量到晶格,导致电阻出现。
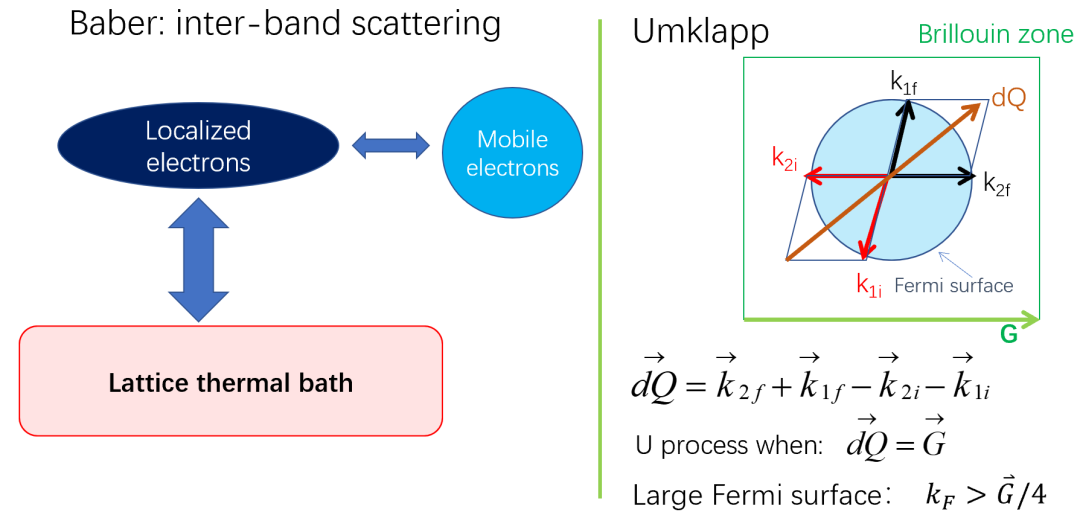
图3 费米液体电子散射机制,左:带间散射;右:Umklapp过程。
Bi2O2Se在动量空间中只存在单一且微小的费米面(图4),不存在上述两种机制起效的基础,所以其电阻率的温度平方关系不能由人们所熟知的费米液体电子散射理论解释。最近也有理论物理学家提出,一些比较特殊的散射机制亦可导致类似行为,例如电子-软声子散射等,但是这种可能性也在本次研究中被排除。

图4 左:Bi2O2Se的能带结构。Bi2O2Se仅在Γ点存在电子能带,所以不存在带间电子散射。
右:布里渊区中心的微小椭圆费米面,无法满足Umklapp过程需求。
这次研究,延续了林效研究员一直以来的科研课题。2015年,他曾在稀释金属SrTiO3中观察到T2电阻率,对现有理论提出挑战[5],引起极大争议,并延续至今。为应对质疑,林效一直在寻找新材料,并最终发现了Bi2O2Se,该体系比起SrTiO3更加简单纯粹。在机理研究上,本次研究更加具备说服力。图5展现了Bi2O2Se和SrTiO3的电阻率温度平方的系数A和费米能EF的相互关系,并将它们与不同费米液体进行比较,发现并无差别。这表明在Bi2O2Se和SrTiO3中,电阻率的温度行为极有可能来自电子-电子散射,其具体机制尚未清楚。
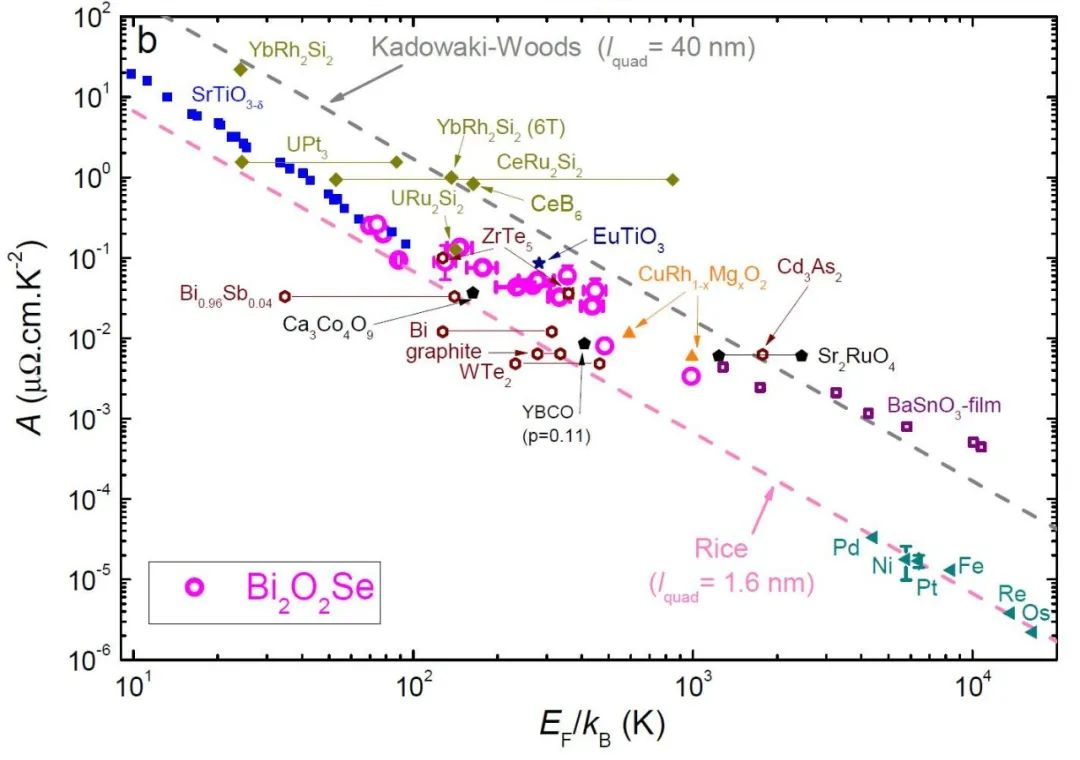
图5 电阻率的温度平方系数A和费米能EF的关系
本次研究对温度平方电阻率的产生机制提出新的问题,促使理论学家深入研究费米液体的电子散射机理。另一方面,Bi2O2Se不仅是性能优越的光电材料,也是下一代高性能、低功耗半导体材料的有力竞争者,理解材料的电子散射机制尤为重要,为基于该材料的电子器件发展打下基础。
论文信息:
https://www.nature.com/articles/s41467-020-17692-6
T-square resistivity without Umklapp scattering in dilute metallic Bi2O2Se.
Jialu Wang, Jing Wu, Tao Wang, Zhuokai Xu, Jifeng Wu, Wanghua Hu, Zhi Ren, Shi Liu, Kamran Behnia & Xiao Lin*
Nat. Commun., 2020,11, 3846, DOI: 10.1038/s41467-020-17692-6
参考文献:
[1] Baber, W.G. The contribution to the electrical resistance of metals from collisionsbetween electrons. Proc. R. Soc. London Ser. A 158, 383-396 (1937).
[2] Rice, M.J. Electron-electron scattering in transition metals. Phys. Rev. Lett. 20,1439-1441 (1968).
[3] Yamada,K. & Yosida, K. Fermi liquid theory on the basis of the periodic AndersonHamiltonian. Prog. Theor. Phys. 76, 621-638 (1986).
[4] Maebashi,H. & Fukuyama, H. Electrical conductivity of interacting fermions. II.Effects of normal scattering processes in the presence of Umklapp scatteringprocesses. J. Phys. Soc. Jpn. 67, 242-251 (1998).
[5] Lin, X., Fauqué, B. & Behnia, K. Scalable T2 resistivity in a small single-component Fermi surface. Science 349, 945 (2015).